Question
Answer: Option A
:
A
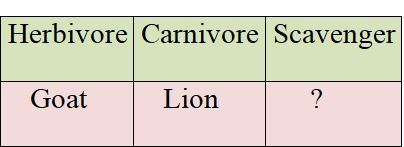
Vultures feed on dead and decayingplants and animals. Animals feeding on dead animalsfall under the category of scavengers.
Was this answer helpful ?
:
A
Vultures feed on dead and decayingplants and animals. Animals feeding on dead animalsfall under the category of scavengers.
Was this answer helpful ?
More Questions on This Topic :
Question 5. Sloths are found in a/an ___ habitat.....
Question 10. ________ help animals in hearing.....
Latest Videos
Latest Test Papers
Submit Solution